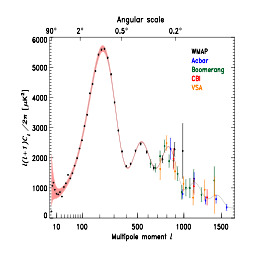
Power spectrum of the cosmic microwave background - a measure of the primordial structure
Within a hot Big Bang model, no structure would form unless some small non-uniformity were present from the start. This initial small fluctuation, Q, in the density then acts as a seed, causing an escalating gravitational collapse. The value of Q must be big enough to result in stars and galaxies. But if Q is too big, the galaxies may be over-crowded which could result in planetary systems which are constantly disrupted by wandering stars. On this basis, Tegmarck and Rees have derived upper and lower bounds on Q consistent with the evolution of planetary life, namely 10^-6 < Q < 10^-4 (compared with the value of ~10^-5 in this universe).
However, this assumes that all other cosmological parameters are unchanged. Tegmark and Rees go on to discuss the implications of also varying the curvature parameter (Omega) and the cosmological constant (Lambda). As mentioned above, structure can form only whilst matter dominates both the curvature and the cosmological constant terms in the Friedmann equation. Since all these terms vary with time (i.e. with the expansion size scale) in different ways, matter only remains dominant for a finite period. The time (or size scale) at which curvature becomes dominant can be found, as can the time for dominance by the cosmological constant. The requirement that the virialisation time (i.e. the time to form structure) be less than these timescales provides two distinct anthropic constraints, one on each of the curvature and the cosmological constant. These can be used to obtain rather loose bounds on the matter-to-photon ratio, which in Tegmark & Rees's definition depends upon the curvature parameter, Omega, as well as the photon:baryon ratio. Although not expressed in this way by Tegmark & Rees, the implication is that the photon:baryon ratio lies between 10^5 and 10^12. Note that the lower bound on the photon:baryon ratio is less restrictive than we derived in CCC11 based on the requirement that the universe avoid being opaque forever (namely >10^6). Thus, overall we can claim the requirement that the photon:baryon ratio lie between 10^6 and 10^12. These rather loose bounds just about rank as a double-sided Type E coincidence.
Tegmark & Rees assume atomic cooling in deriving their lower bound for Q. They dismiss molecular cooling as irrelevant to their argument. In contrast, in the Cold Big Bang alternative universe of Aguirre (2001), as discussed in CCC11B, structure formation occurs through molecular cooling mechanisms. Aguirre claims that these molecular mechanisms are efficient under the conditions of higher density and lower temperatures prevailing in his universe. This is what allows structure to form in the Aguirre universe even though Q is only 10^-11 to 10^-8, in gross violation of the above bound. The photon:baryon ratio in the Aguirre universe is of order unity, so Aguirre is considering a distance region of parameter space.
Tegmark & Rees also derive the upper limit on the cosmological constant consistent with structure formation (i.e. consistent with matter dominance over the virialisation timescale). They find it to be proportional to Q^3. Thus, increasing Lambda by a factor of 10^6 can be offset by increasing Q by a factor of 100. In such a universe, galaxy formation would be complete in a few million years. Thereafter the universe would expand exponentially under the influence of the dominant Lambda. Between then and now it would inflate by a factor of ~e^100, with the consequence that our galaxy would be the only thing in the observable universe.
This final observation of Tegmark and Rees is of particular significance since it undermines, or substantially weakens, the arguments of Martel et al discussed in CCC12A. Martel et al derived the most likely value for the cosmological constant consistent with the anthropic constraint. However, they did so assuming all other cosmological parameters were invariant. Tegmark & Rees point out that this is invalid, since variations in Lambda by some factor f can be neutralised by assuming a simultaneous variation of Q by a factor f^1/3. Whilst Tegmark & Rees's bounds on Q are relatively tight in the context of order-of-magnitude estimates, i.e. one order of magnitude either way, this still permits a variation by a factor of 1000 either way in Lambda to be accommodated without anthropic disadvantage. This suggests that the arguments of Martel et al should really be re-evaluated based on a bivariate probability distribution over both Lambda and Q. It is likely that this would severely weaken the claim that the anthropic constraint is sufficient to plave Lambda close to its observed value.
Go to Cosmic Coincidences Next Chapter Abstract
Go to the Cosmic Coincidences Chapter Selection Page
Go to the Cosmology Tutorial page
Go to Rick's Cosmology FAQ
Go back to Rick's Home Page (Main Menu)
Contact me and other links

Power spectrum of the cosmic microwave background - a measure of the primordial structure